Efficient Convolutional Neural Network with MobileNet
Reduce CNN operations with depth-wise and point-wise convolutions
Problem
The number of operations of convolution is quite resource-intensive. Suppose we have an input image of size \(D_x \times D_x \times M\) and a convolution block with a kernel of size \(D_k \times D_k \times M\). First, the conv block will do element-wise multiplication with a segment on the input image. Then, we sum the value along all the channels into a single value. The kernel then slides by one block to the right (if the stride is 1), and the whole process is repeated until all ceils are covered. \(N\) kernel is used to obtain \(N\) channel as output.

Regular Convolution (Source: https://towardsdatascience.com/a-basic-introduction-to-separable-convolutions-b99ec3102728)
Operations of a regular Conv block are:
One Conv Block's Operations: \(D_k \cdot D_k \cdot M\)
One Block's Slide over the input: \(D_x \cdot D_x\)
Using \(N\) conv blocks, the total operation is:
$$T = D_k \cdot D_k \cdot M \cdot D_x \cdot D_x \cdot N$$
Solution
One key challenge is that the conv multiplication is repeated for all \(N\) blocks. For example, one conv block is applied to the top-left corner of the input. The second block will re-compute everything again. The idea of a Depth-wise separable convolution block is to not repeat that element-wise multiplication.
Each of the regular conv blocks does multiplication followed by additions. In depth-wise separable convolution, the process is split into two. One layer is for multiplication and another is for addition.
- Depthwise Convolution: This is similar to regular conv block except it does not perform additional across all channels. Hence, the operation is \(D_k \cdot D_k \cdot M \cdot D_x \cdot D_x\).
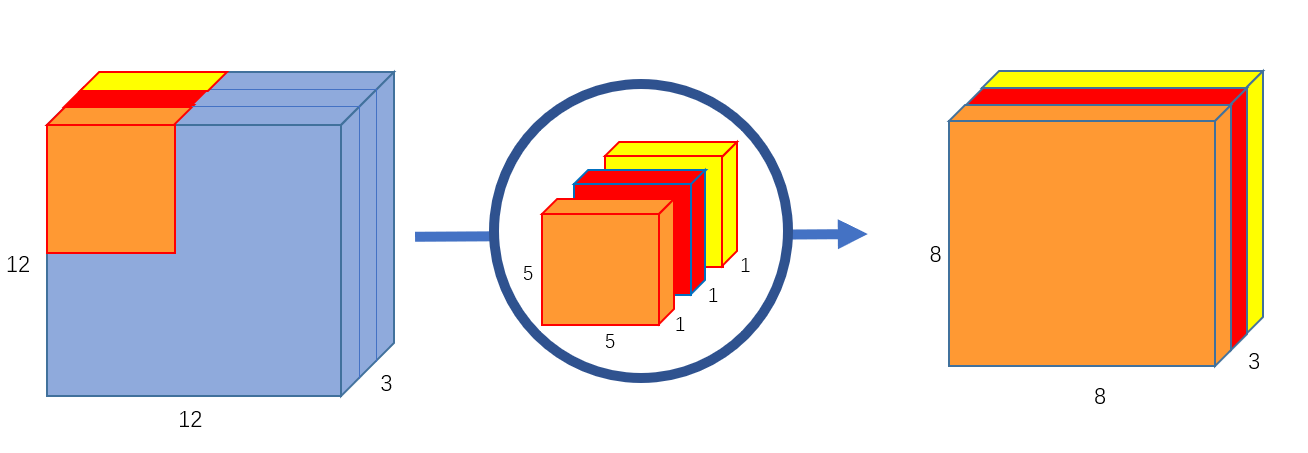
Depthwise Convolution (Source: https://towardsdatascience.com/a-basic-introduction-to-separable-convolutions-b99ec3102728)
- Pointwise Convolution: This is a \(1 \times 1 \times M\) kernel. \(N\) kernels are used to obtain \(N\) channels as output. The number of operations: \(D_x \cdot D_x \cdot M \cdot N\).
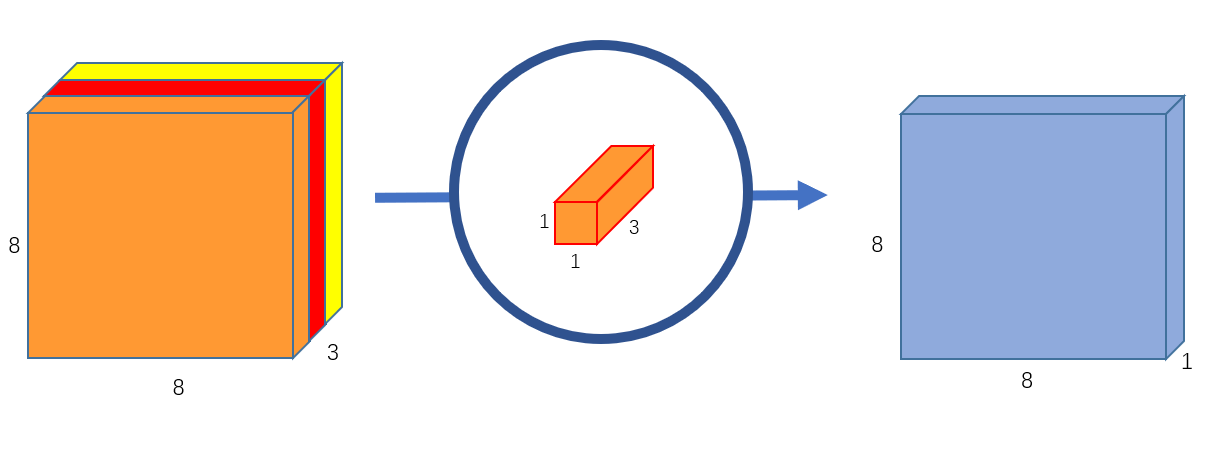
Pointwise Convolution (Source: https://towardsdatascience.com/a-basic-introduction-to-separable-convolutions-b99ec3102728)
Total operations of Depth-wise Separable Convolution:
$$(D_k \cdot D_k \cdot M \cdot D_x \cdot D_x) + (D_x \cdot D_x \cdot M \cdot N)$$
Let's compare:
$$\frac{(D_k \cdot D_k \cdot M \cdot D_x \cdot D_x) + (D_x \cdot D_x \cdot M \cdot N)}{D_k \cdot D_k \cdot M \cdot D_x \cdot D_x \cdot N} =\frac{1}{N} + \frac{1}{D_k \cdot D_k}$$
Here we can see that the depth-wise approach requires way fewer operations than the regular conv block.
How to use
Instead of using a regular convolution layer, we use two separate operations - depthwise and pointwise convolutions.
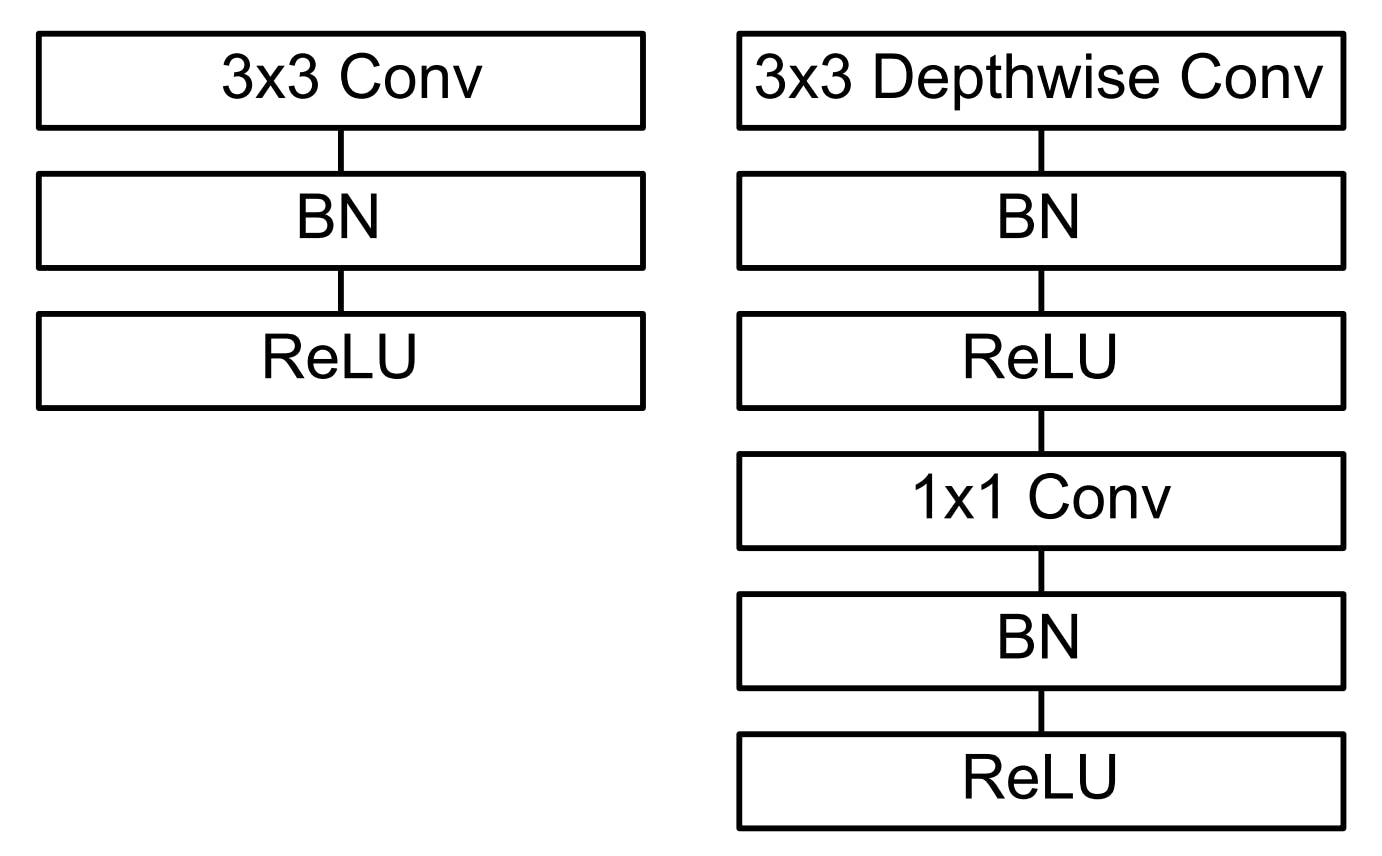
Regular Conv vs. Depthwise Separable Conv (Source: Original research paper)
